Earth Curvature Calculator
Accurately calculate the curvature you are supposed to see on the ball Earth.
| Distance | Curvature |
|---|---|
| 1 km | 0.00008 km = 0.08 meters |
| 2 km | 0.00031 km = 0.31 meters |
| 5 km | 0.00196 km = 1.96 meters |
| 10 km | 0.00785 km = 7.85 meters |
| 20 km | 0.03139 km = 31.39 meters |
| 50 km | 0.19620 km = 196.20 meters |
| 100 km | 0.78479 km = 784.79 meters |
| 200 km | 3.13897 km = 3138.97 meters |
| 500 km | 19.6101 km = 19610.09 meters |
| 1000 km | 78.3196 km = 78319.62 meters |
| Distance | Curvature |
|---|---|
| 1 mile | 0.00013 miles = 0.67 feet |
| 2 miles | 0.00051 miles = 2.67 feet |
| 5 miles | 0.00316 miles = 16.67 feet |
| 10 miles | 0.01263 miles = 66.69 feet |
| 20 miles | 0.05052 miles = 266.75 feet |
| 50 miles | 0.31575 miles = 1667.17 feet |
| 100 miles | 1.26296 miles = 6668.41 feet |
| 200 miles | 5.05102 miles = 26669.37 feet |
| 500 miles | 31.5336 miles = 166497.53 feet |
| 1000 miles | 125.632 miles = 663337.65 feet |
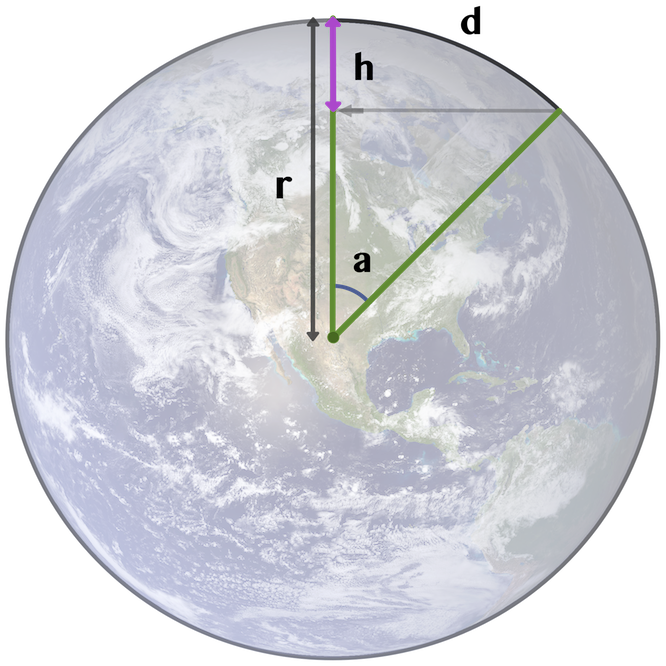
Explanation:
The Earth's radius (r) is 6371 km or 3959
miles, based on numbers from
Wikipedia,
which gives a circumference (c)of
c = 2 * π * r = 40 030 km
We wish to find the height (h) which is the
drop in curvature over the distance (d)
Using the circumference we find that 1 kilometer has the angle360° / 40 030 km = 0.009°. The angle (a) is then
a = 0.009° * distance (d)
The derived formula h = r * (1 - cos a) is accurate for
any distance (d)